1
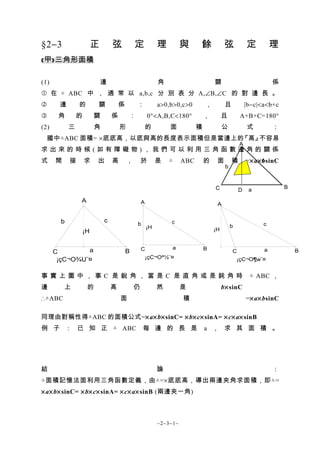
正十二面体の表面積、体積そして半径（内接円と外接円)を計算する前に、球を利 用して正十二面体を形成することを考えましょう。 正多面体の一つの頂点に対して 三つの正三角形や四つの正三角形が集まる形だと、それぞれ、正四面体や正八 面体にしかならないので、五つの正三角形がA=面積 a=面積 a=面積 もし とすれば a=面積 a=面積 もし とすれば a=面積 p=楕円の周囲 a=πab 、pを求める近似式 a=面積 a=面積bcd a=面積 なお点線に示すよう二つの三角形となし 各々の面積を計算しその和をもって 不平行四辺形の面積を算出してもよい =弧の
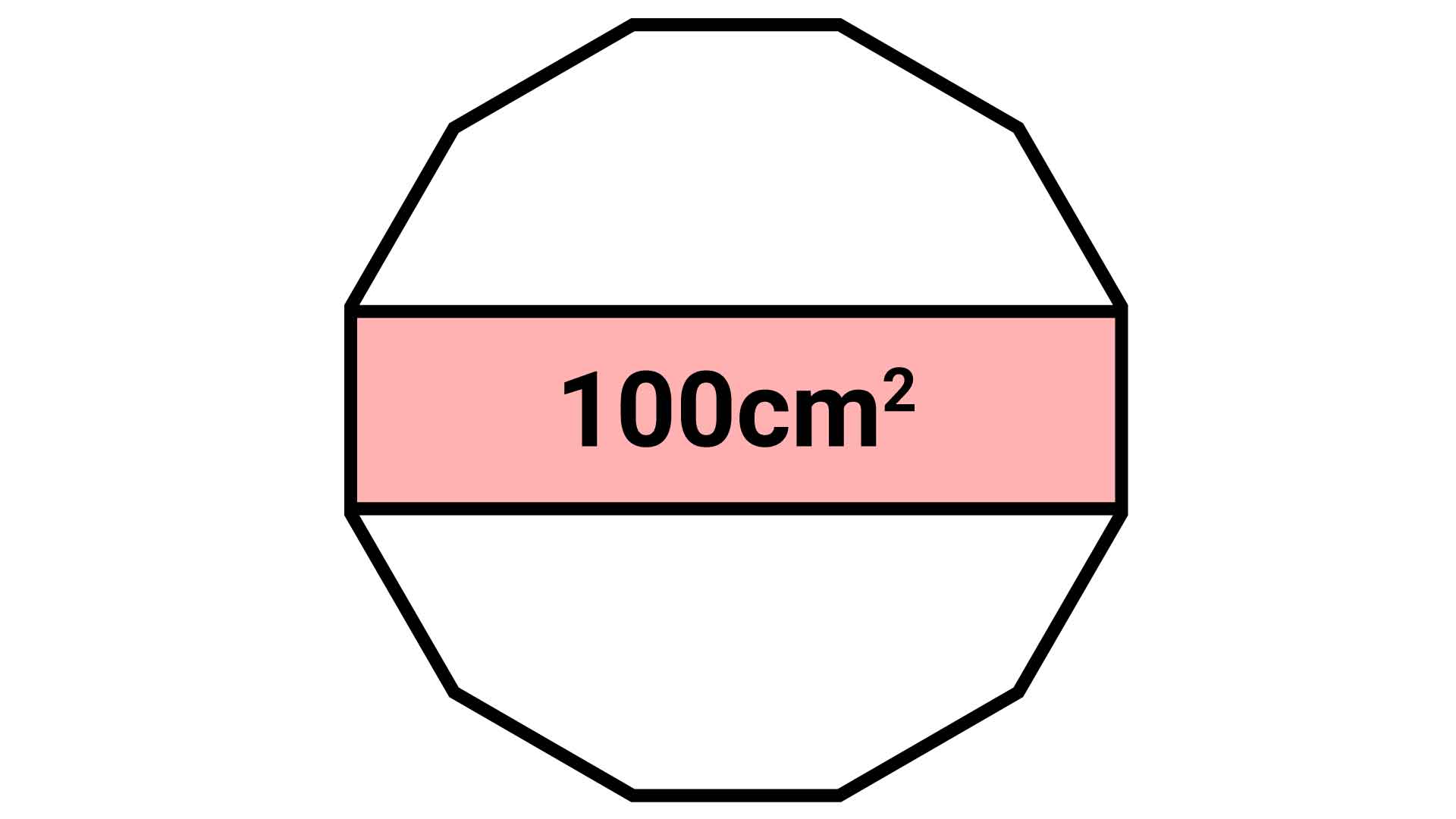
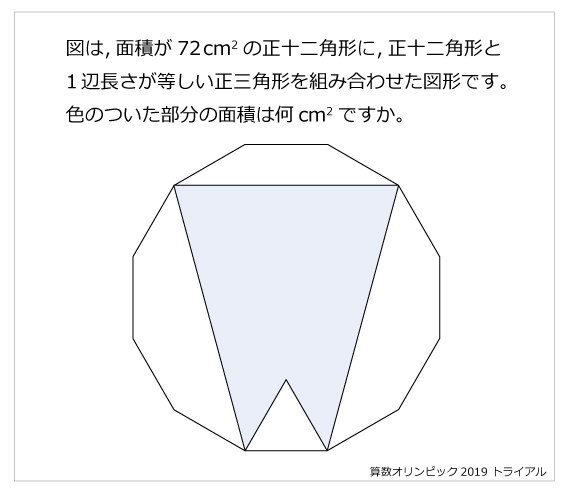
正12角形 面積 半径
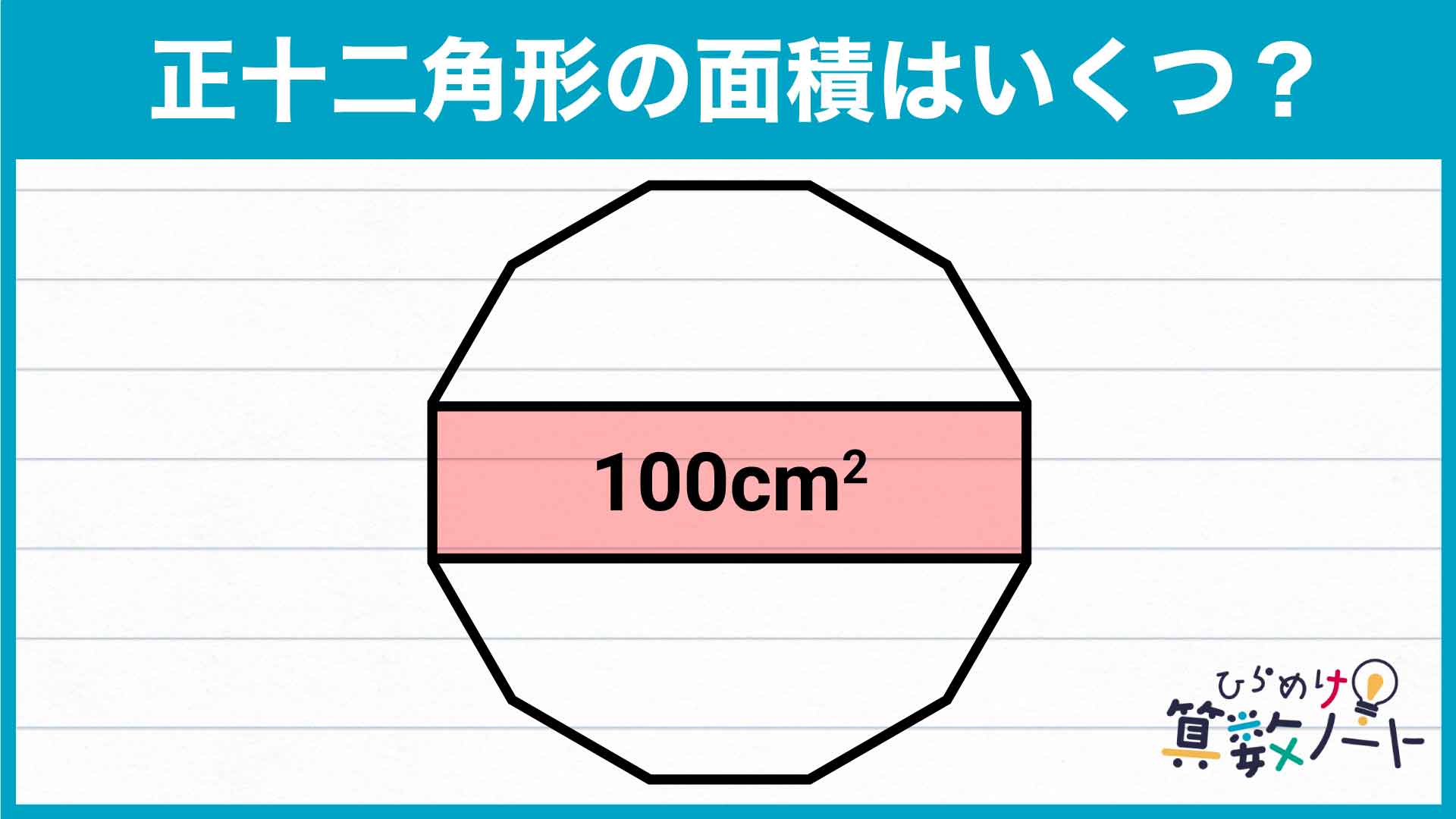
正12角形 面積 半径-参考 図1：正十二角形は 個の正方形と 個の正三角形に分割できるから，面積は 図2：図のように， つに分割して並べ替えると を一辺とする正方形になる。円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 1辺フラット 円
三角形 21 直角三角形面積的基本計算題 Youtube
8 rows 六角形 6角形 面積計算 公式 求め方 対辺 ヘキサゴン 自動 直径 内接 外接 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 鈍角三角形の数を数える 鈍角三角形の鋭角のうちの1つをa 1 とする。 残りの頂点は「a 2 ～a 6 から2つ」または「a 8 ～a 12 から2つ」選べばよい。（鈍角の円周角に対する中心角は180°より大きいから） よって 5 c 2 ×2=通り。 頂点の選び方が12通りあるから240今回の記事では、 上のような2パターンの 正八角形の面積を求める方法 について解説していきます。 この問題を解くためには中学3年生で学習する「三平方の定理」の知識が必要となります。 ⇒ 三平方の定理覚えておきたい基本公式を解説！
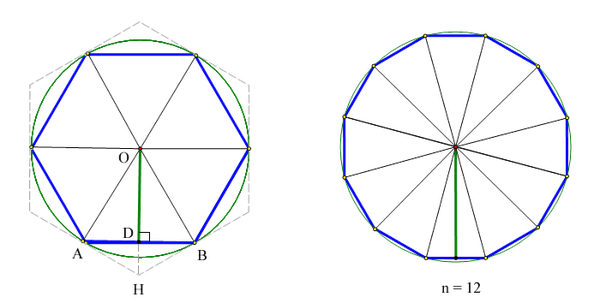
正12角形の面積 半径2の円に内接する正12角形の面積を求めよ。解き方教えてください！ （360度÷12＝30度） ここで三角比の三角形の面積を求める公式を使って、 12等分された三角形の一つの面積を求めますと･･･ 1/2×2×2×sin30°＝1 これが12個あるわけ正12角形の作図 正六角形を作図する要領で円周を6等分します。さらにこれを二等分すれば12等分したことになります。 この作図の証明ファイルはありません。 正12角形の作図のアニメーション 参考 正6角形の作図 top プライバシー 三角形の面積が 式から 底辺が同じ長さで高さが同じなら面積は同じであることがわかります。 正多角形を適当にいくつかの三角形に分けます。 例えば、正五角形の場合で言えば、3つに分けれます。 1つの辺を基準の辺として、延長線を引きます。
正12角形 面積 半径のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw | Ime Ntnu Edu Tw |
Ime Ntnu Edu Tw | Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |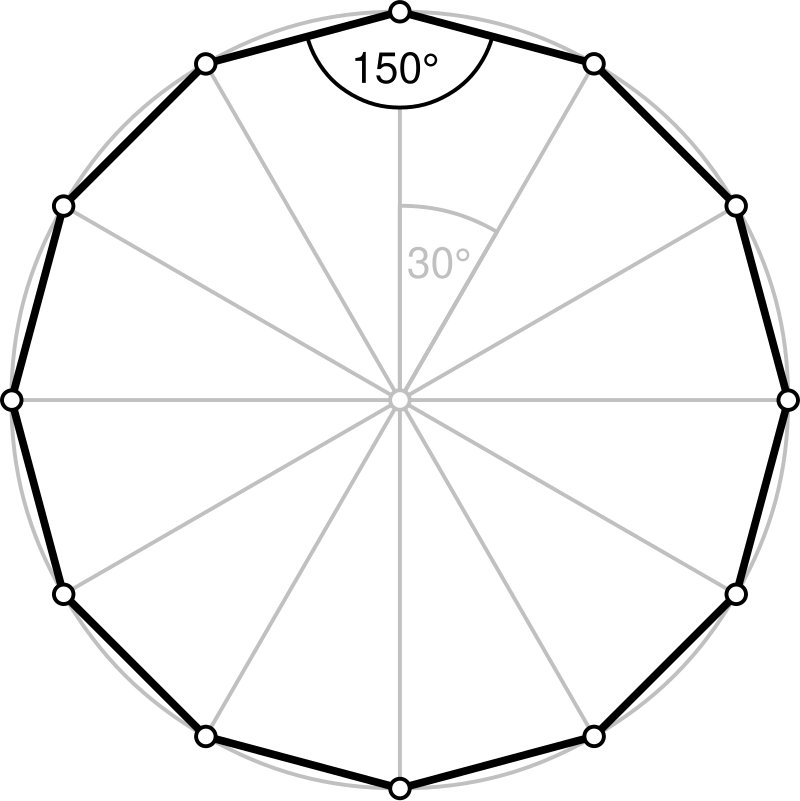
 Ime Ntnu Edu Tw | Ime Ntnu Edu Tw | Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw | Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw | Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
Ime Ntnu Edu Tw | 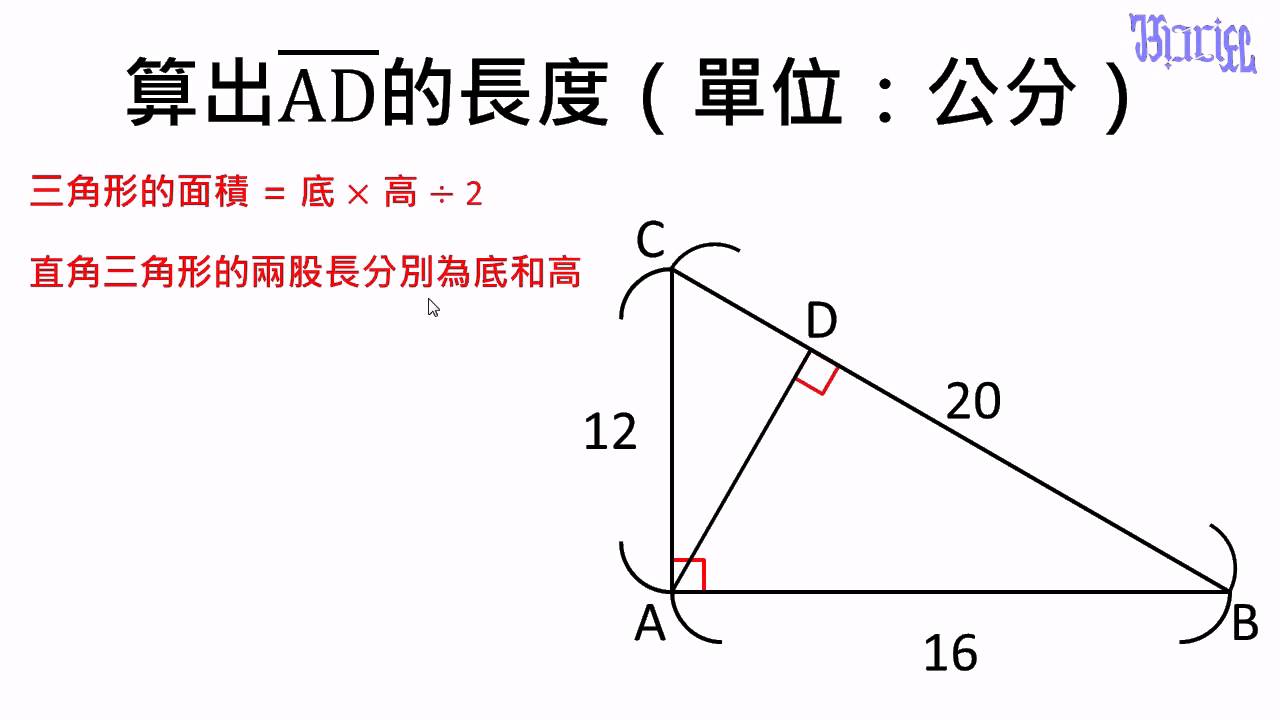 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw | Ime Ntnu Edu Tw |
Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |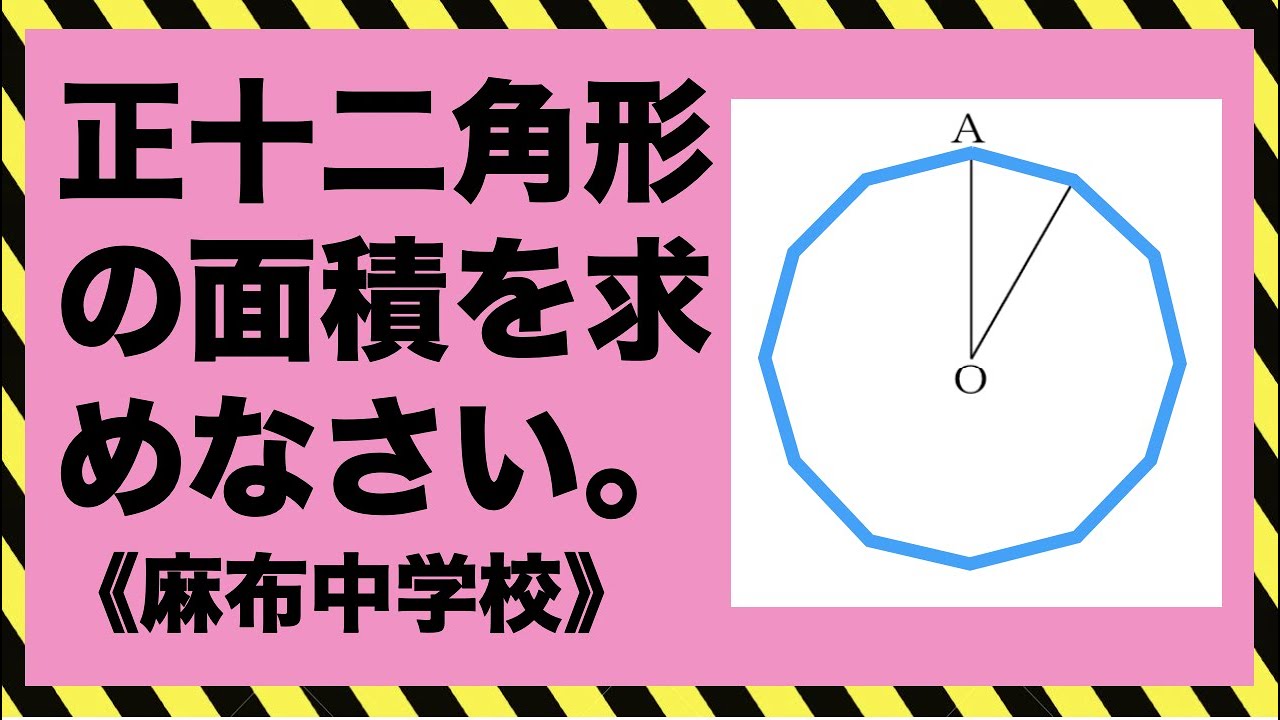
Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw | Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw | Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw | Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw | Ime Ntnu Edu Tw |
Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
 Ime Ntnu Edu Tw |  Ime Ntnu Edu Tw |
面積は当然、底辺×高さ× で求められるので、以下の通りです。 こうした一般的な解き方でも1分以内に解答したいところですが、今回教える2大公式によって高さ2秒、面積3秒、合わせて5秒で答えを出すことができます。 その公式がこちらです。 aに正正十二角形の対角線の長さ・面積 正十二角形の 辺の長さを ，外接円の半径を ，内接円の半径を とする。 つの辺たとえば に対する弧 の中心角は ，円周角は ， 正十二角形の内角は ，外角は である。 ， は直角三角形であるから
Incoming Term: 正12角形 面積, 正12角形 面積 小学生, 正12角形 面積 中学受験, 正12角形 面積 半径,
0 件のコメント:
コメントを投稿